ما هو ال Big O؟

هي حالات نقيم أو نقيس أداء الكود من خلالها بناء علي وقت أو سرعة تنفيذ البرنامج و مساحته في ذاكرة التخزين العشوائي (RAM) ونركز في الأغلب علي وقت التنفيذ.

ينقسم الBig O إلي حالات متعددة تبدأ من أفضل أداء للكود إلي أسوء وكلما إرتفع المقياس أصبح برنامجنا في حالة يرثى لها.

1.Constant Time - o(1)

دعنا ننظر لهذه الصورة ونتأملها معاً

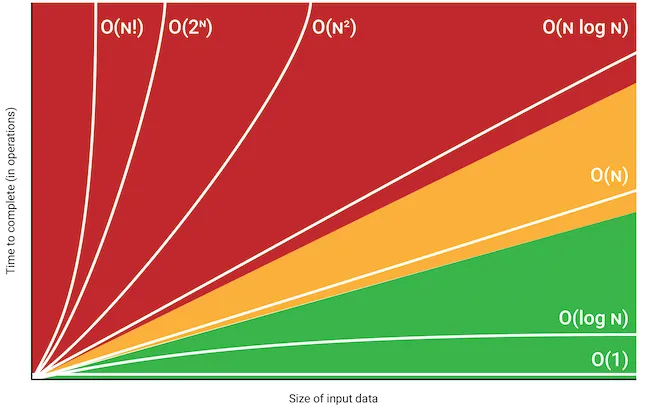
كما يظهر لنا من تدرج الألوان كلما إرتفع عدد العمليات تصبح حالة البرنامج أسوء فكلما دخل المترجم الخاص باللغة في عدد من العمليات المتكررة أصبحت حالته أسوء فنحن نعتمد علي عمليات التكرارات لهذا نجد أن المتغييرات والشروط والدوال تكون حالتها o(1) أي ثابتة لا ترتفع.

const names = ["Hozaifa","Abdelrahman","Shaheen"];

function printFun(name){ // o(1)
console.log(name[0])
}
printFun(names)

هذا البرنامج قام بإجراء عملية طباعة ووصل بشكل مباشر من خلال رقم العنصر أو رقم الإدخال الموجود داخل المصفوفة فاهو أجري عملية واحدة في الوصول ومن ثم طبع الناتج فتكون حالته o(1) أي وقت ثابت (constant time) وهذا بالنسبة لنا أفضل حالة قد يأخذها برنامجك وكذلك لم ينظر ولم يهتم بما يوجد داخل المصفوفة حتي وإن كان مليون عنصر فلم يهتم لعدد الإدخالات بل إهتم بما سينفذه وهو طباعة أول عنصر لهذا تبقي حالته ثابتة.

• لمشاهدة مثال أخر إضغط هنا

2.Logarithmic Time - o(log n)

في هذه الحالة سيكون هناك تكرار للحالات لكن لن يكون بشكل خطي أي لن تكون الحالات واحد اثنين ثلاث هكذا بل في كل مرة يتضاعف الرقم من واحد إلي اثنين ومن إثنين إلي أربعة ومن أربعة إلي ثماني حتي يصل للشرط المطلوب بشكل أسرع بالتالي عدد العمليات يتقلص ويمكنك فهمها من خلال هذا المثال

let N = 8, k = 0;

// First loop run N/2 times
for (let i = parseInt(N / 2); i <= N; i++) {
// Inner loop run log N

// times for all i
for (let j = 2; j <= N;j = j * 2) {
// Print the value k
console.log(k +" ");

k = k + parseInt(N / 2);
}}

• لمشاهدة مثال أخر إضغط هنا

3.Linear Time - o(n)

هذه الحالة مثالية بعض الشئ نظراً لأنك ستستخدم الكثير من هياكل البيانات التي تأخذ هذه الحالة ولكي أُيقظك أعد النظر لتلك الصورة

كما تري أن o(n) لونها أصفر وضع في عقلك أنها تعتبر من الحالات المثالية رغم أنها ليست كذلك إن قارنتها بمن سبقها وهذه الحالة مشابهة للحالة السابقة o(log n) لكن بدل من مضاعفة نفسها تأخذ تعدادها بشكل خطي أي واحد اثنين ثلاث أربع إلخ.. ولكي تفهمها إنظر لهذا الرمز:

function findMax(arr) {
let count = 0;

for (let i = 0; i < arr.length; i++) {
count++;
}
return `Inputs: ${arr.length}\noperations: ${count}`;
}
console.log(findMax([4, 6, 7, 8, 6, 2]));
// Inputs: 6 operations: 6

• لمشاهدة مثال أخر إضغط هنا

4.Linearithmic Time - o(n log n)

هذه الحالة بالنظر إلي الصورة التالية فإن تلك الحالة تكمن نتيجتها من خلال جمع الحالتين السابقتين o(n) و o(log n) أي أننا نجمع 1 + .5 فيكون الناتج 1.5. وغالباً تحدث نتيجة استخدم خوارزمية حالتها o(n) مع خوارزمية من حالة o(log n) مثل هذا المثال

// Merge

function merge(arr1 = [],arr2 = []){ // o(n)

const merged = [];

let arrOneIndex = 0;

let arrTwoIndex = 0;

while(arrOneIndex < arr1.length || arrTwoIndex < arr2.length){

if(arrOneIndex >= arr1.length || arr1[arrOneIndex] > arr2[arrTwoIndex]){

merged.push(arr2[arrTwoIndex]);

arrTwoIndex+=1;

}else{

merged.push(arr1[arrOneIndex]);

arrOneIndex+=1;
}
}

return merged;
}

// Sort

function sort(arr = []){ // o(n log n) (sort + merge)
const size = arr.length;

if(size<2) return arr;

if(size === 2){
return arr[0] > arr[1] ? [arr[1], arr[0]] : arr;
}

const mid = parseInt(size / 2, 10);

return merge(sort(arr.slice(0,mid)),sort(arr.slice(mid)))
}

console.log(sort([4,2,5,6,77,55]))

5. Quadratic Time - o(n ^2)

في هذه الحالة الكود يتضاعف بشكل تربيعي أي إن كان لدينا تكرار بداخله تكرار ويزداد بشكل خطي فأهلا بك في o(n ^2) ورقم 2 جاء بناء علي التكرار فكما قلت تكرار بداخله تكرار إذا لدينا تكرارين فقط أي 2 و n هو المدخلات التي سيقرأها التكرار بناء عليه سيتوقف ويمكنك فهمها من خلال ضرب التكرار الرئيسي في الداخلي وستفهمها بشكل أوضح من هذا المثال

const chars = ["a","b","c","d"]

function printFor(arr){

let operations = 0;

for(let i= 0; i < arr.length;i++){ // o(n)

for(let j = 0; j < arr.length;j++){ // o(n)
operations++;

console.log(arr[i],arr[j])
}
}

console.log(`Input= ${arr.length}\nOperations= ${operations}`)
}



printFor(chars) // o(n ^2) || o(i*j)